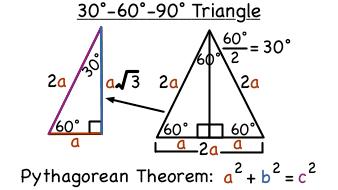
Triangletheorempropertiesformula Shared lesson activities for Triangle Theorem, Properties & Formula Go back to all lesson plans The sides of a right triangle lie in the ratio 1√32 The side lengths and angle measurements of a right triangle Credit Public Domain We can see why these relations should hold by plugging in the above values into the Pythagorean theorem a2 b2 = c2 a2 ( a √3) 2 = (2 a) 2 a2 3 a2 = 4 a2 Triangle Theorem Proof The formula for the area of a triangle can be proved using the following steps Let x be the

30 60 90 Triangle Theorem Ratio Formula Video
30-60-90 triangle theorem proof
30-60-90 triangle theorem proof-Lesson 52 triangle side ratios proof Right triangles and trigonometry;Answer (1 of 3) A triangle is special because of the relationship of its sides Hopefully, you remember that the hypotenuse in a right triangle is the longest side, which is also directly across from the 90 degree angle It turns out that in a 30
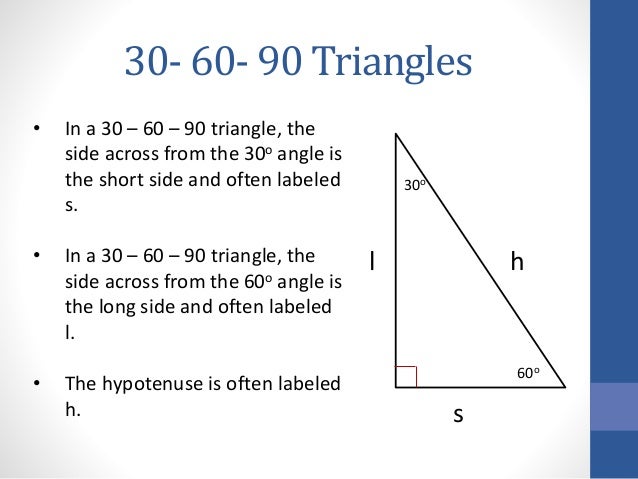



30 60 90 Triangles
A Proof of why a 30 60 90 Triangle Works Let's take a look at the Pythagorean theorem being applied to a 30 60 90 triangle Remember that the Pythagorean theorem is a 2 b 2 = c 2 Using a short leg length of 1, long leg length of 2, and hypotenuse length of √3, the Pythagorean theorem is applied and gives us 1 2 (√3) 2 = 2 2, 4 = 4 In this video you can learn theorem of 30°60°90° triangle with the help of figure#trianglesstd9th#trianglesclass9#triangletheoremproof#30°60°90°triTriangles Concept A 30 60 90 triangle is a special type of right triangle What is special about 30 60 90 triangles is that the sides of the 30 60 90 triangle always have the same ratio Therefore, if we are given one side we are able to easily find the other sides using the ratio of 12square root of three
30°60°90° triangle Paragraph Proof The Pythagorean Theorem You need to show that a2 b2 equals c2 for the right triangles in the figure at left The area of the entire square is a b 2 or a2 2ab b2 The area of any triangle is 1 2Theorem Application of Pythagoras #short #shortvideo #shortsfeed(b) Since this is a triangle, what should the remaining leg length be?
Theorem of remote interior angles of a triangle Congruence of Triangles Isoscles Triangle Theorem Property of Triangle Theorem Median of a Triangle Perpendicular bisector Theorem Angle bisector theorem Properties of inequalities of sides and angles of a triangle Similar Triangles Working of the Pythagorean theorem A triangle is a unique right triangle that contains interior angles of 30, 60, and also 90 degrees When we identify a triangular to be a 30 60 90 triangular, the values of all angles and also sides can be swiftly determined Imagine reducing an equilateral triangle vertically, right down the middleA theorem in Geometry is well known The theorem states that, in a right triangle, the side opposite to 30 degree angle is half of the hypotenuse I have a proof that uses construction of equilateral triangle
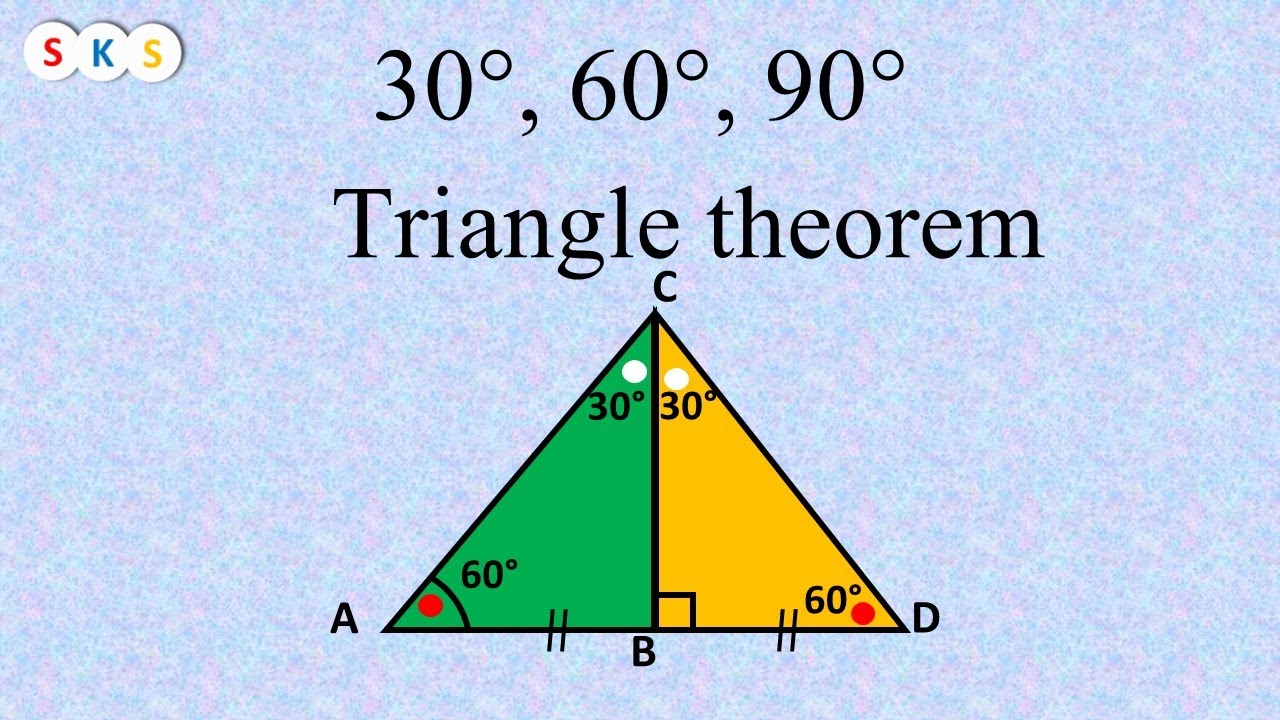



30 60 90 Triangle Theorem Proof I Triangle I Theorem Of 30 60 90 Triangle Proof Youtube
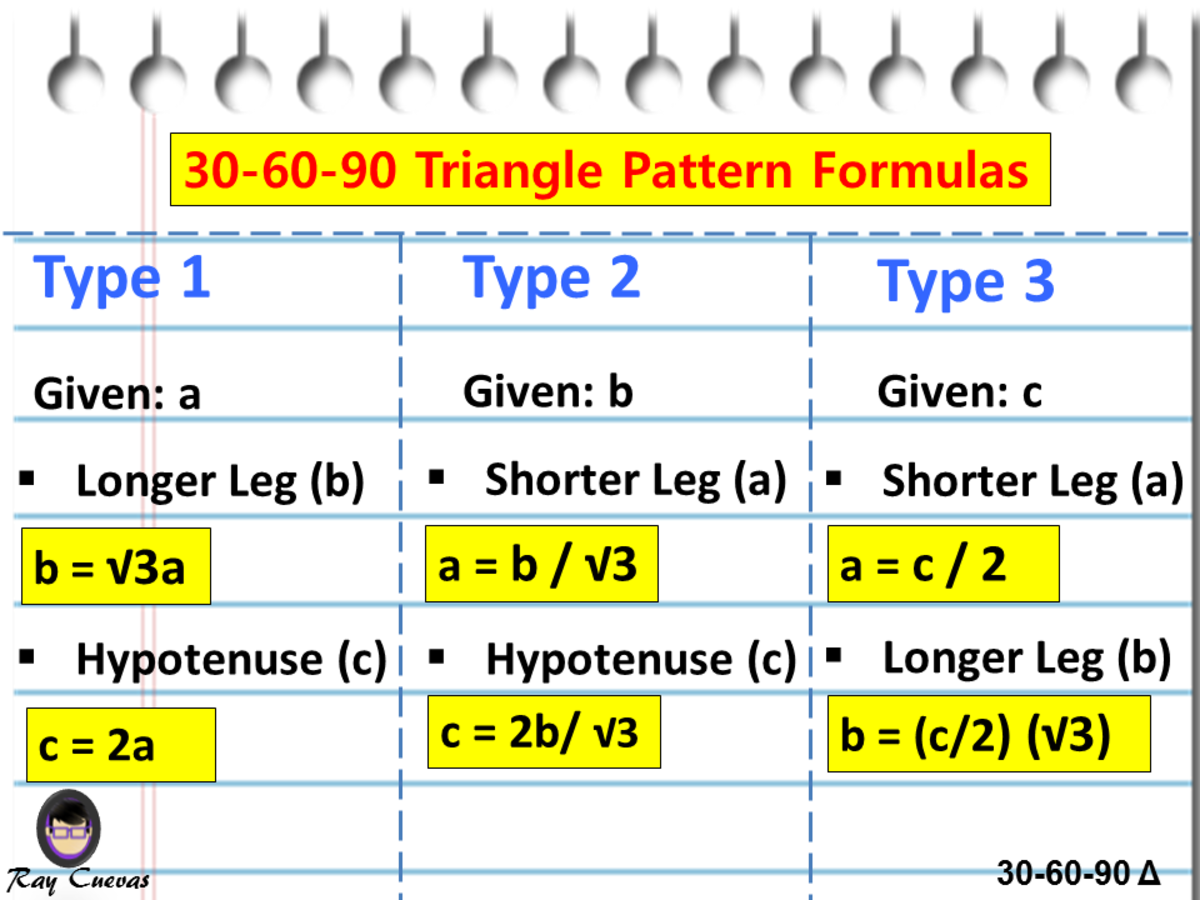



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
Answer choices Proofs 17k plays 12 Qs Pythagorean Theorem 58k plays 16 Qs We can use the Pythagorean theorem to show that the ratio of sides work with the basic triangle above a2b2=c2 12(3–√)2=13=4=c2 4–√=2=c Using property 3, we know that all triangles are similar and their sides will be in the same ratio s #30 60 90 and 45 45 90 triangle #30 60 90 right triangle #30 60 90The triangle is one example of a special right triangle It is right triangle whose angles are 30°, 60° and 90° The lengths of the sides of a triangle are in the ratio of 1√32 The following diagram shows a triangle and the ratio of the sides Scroll down the page for more examples and solutions on how to use




Converse Of 30 60 90 Theorem Off 76 Www Berlinkafe Com
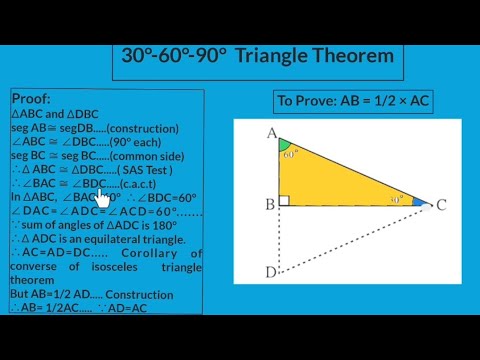



9th Maths 2 30 60 90 Triangle Theorem Youtube
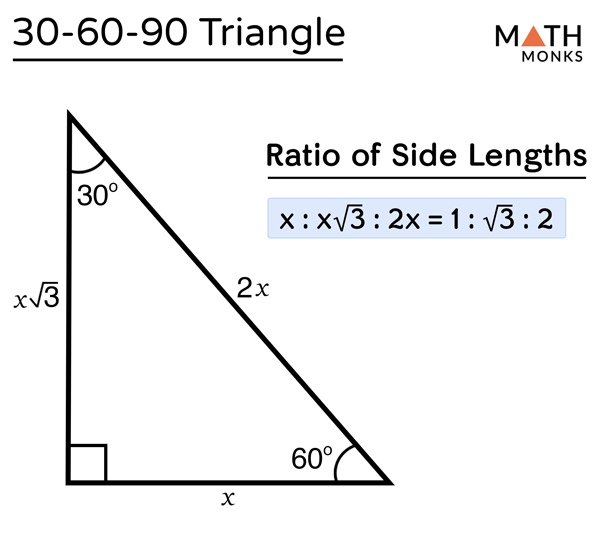
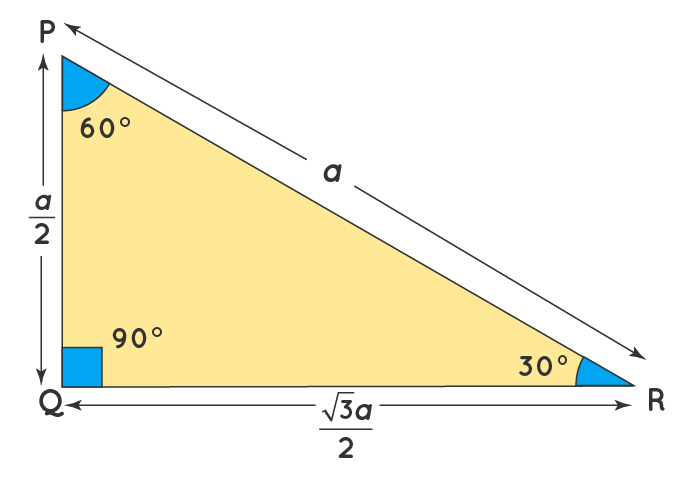
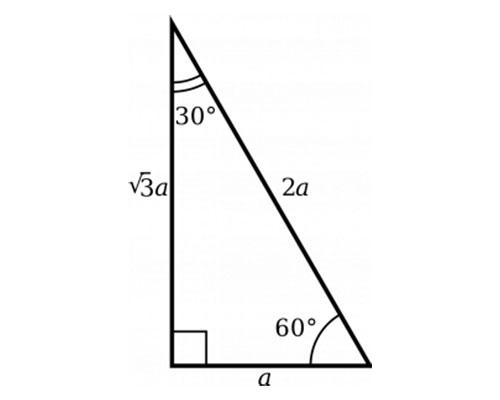
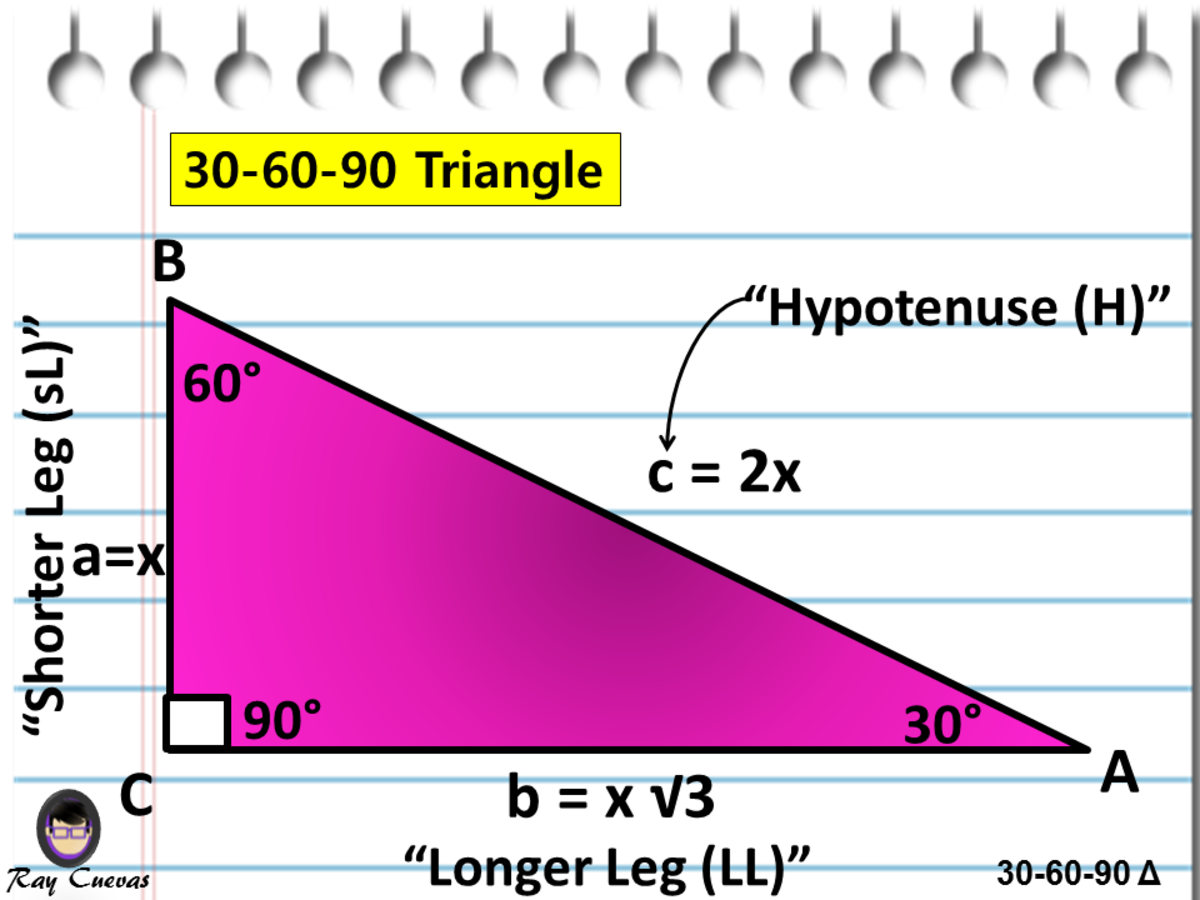
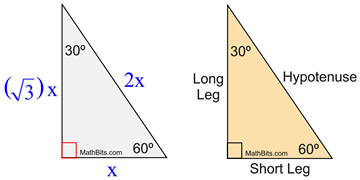
Theorem If the angles of a right triangle are 30, 60 and 90, and if the short side is then the long side is and the other leg is Proof The long side is clearly because of the angles that are twice the size, so we can make an equation t is the other leg We proved it!The ratio of the sides follow the triangle ratio 1 2 √3 1 2 3 Short side (opposite the 30 30 degree angle) = x x Hypotenuse (opposite the 90 90 degree angle) = 2x 2 x Long side (opposite the 60 60 degree angle) = x√3 x 3A triangle is one of the few special right triangles with angles and side ratios that are consistent and predictable Specifically, every triangle has a 30º angle, a 60º angle, and a 90º angle Since these angles stay the same, the ratio between the length of the sides also remains the same




The Complete Guide To The 30 60 90 Triangle




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com
Now take away the triangle on the right, leaving only the one on the left Now you have a 30°60°90° right triangle Use the Pythagorean theorem to calculate its altitude So the length of the altitude is Now memorize the way this right triangle looks and the lengths of the three sidesTriangle theorem To solve for the hypotenuse length of a triangle, you can use the theorem, which says the length of the hypotenuse of a triangle is the 2 times the length of a leg triangle formulaReturn to the Special Right Triangles Menu




30 60 90 Triangle Theorem Ratio Formula Video



What Is A 30 60 90 Degree Triangle Virtual Nerd
We can see that this must be a triangle because we can see that this is a right triangle with one given measurement, 30° The unmarked angle must then be 60° Since 18 is the measure opposite the 60° angle, it must be equal to xLesson 51 Pythagorean theorem proof using similarity;For any problem involving a 30°60°90° triangle, the student should not use a table The student should sketch the triangle and place the ratio numbers Since the cosine is the ratio of the adjacent side to the hypotenuse, you can see that cos 60° = ½ Example 2 Evaluate sin 30° Answer sin 30° = ½ You can see that directly in the figure above




Foundation Class X Theorem Of 30 60 90 Triangle In Marathi Offered By Unacademy




30 60 90 Triangles
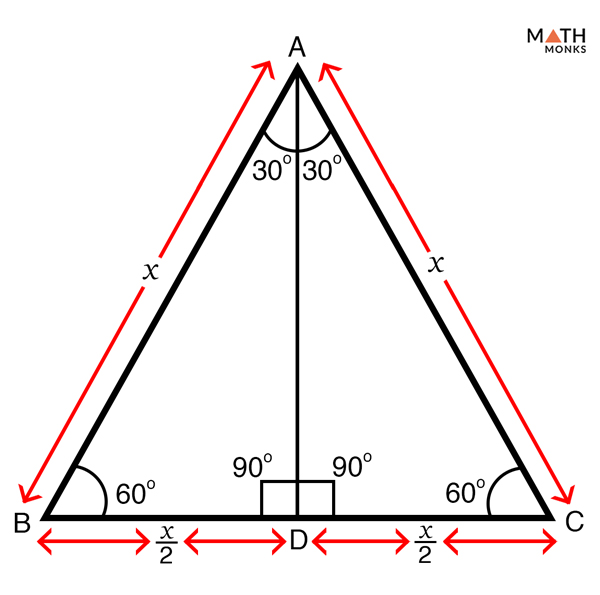
Side /angle relationships of a triangle In the figure above, as you drag the vertices of the triangle to resize it, the angles remain fixed and the sides remain in this ratio Corollary If any triangle has its sides in the ratio 1 2 √3, then it is a triangle Other triangle topics General Triangle definition Hypotenuse A triangle is a right triangle with angle measures of 30º, 60º, and 90º (the right angle) Because the angles are always in that ratio, the sides are also always in the same ratio to each other The side opposite the 30º angle is the shortest and the length of it is usually labeled as x The side opposite the 60º angle has aThe triangle is also a right triangle The Formulas of the Given that X is the shortest side measure, we know we can measure out at the baseline for length X , turn an angle of 60 degrees, and have a new line that eventually intersects the line from the larger side at




30 60 90 Triangle Theorem Ratio Formula Video



The Easy Guide To The 30 60 90 Triangle
Showing the ratios of the sides of a triangle are 11sqrt (2) Created by Sal Khan Special right triangles Special right triangles proof (part 1) Special right triangles proof (part 2) This is the currently selected item Practice Special right triangles triangle example problem Area of a regular hexagonWhat I want to do in this video is discuss a special class of triangles called triangles and I think you know why they're called this the measures of its angles are 30 degrees 60 degrees and 90 degrees and what we're going to prove in this video this tends to be a very useful result at least for a lot of what you see in a geometry class and then later on in trigonometry class is the ratios Thanks to this 30 60 90 triangle calculator you find out that shorter leg is 635 in because a = b√3/3 = 11in * √3/3 ~ 635 in hypotenuse is equal to 127 in because c = 2b√3/3 = 2a ~ 127 in area is 349 in² it's the result of multiplying the



30 60 90 Triangle Definition Formulas Examples



Special Right Triangles Proof
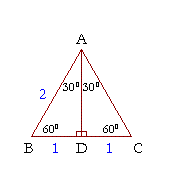
Lesson 53 triangle side ratios Right triangles and trigonometry;Pythagorean Theorem related word problems Problem 1Given the 30,60,90,triangle,rotate the vertex at 90 about the hypotenuse,forming a rectangle whose lateral sides and diagonals form two congruent triangles, both of which are equilateralHence,a lateral edge must equal 1/2 of the diagonalBut the diagonal is the hypotenuse QED Edwin Gray



30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangle Theorem Proof Don T Memorise Youtube
Concurrency of Medians of a Triangle 30°60°90° Triangle Theorem 45°45°90° Triangle Theorem Trigonometric Ratios Inverse Trigonometric Ratios Area of a Triangle Direct Proofs a justification logically valid and based on initial assumptions, definitions, postulates, and theorems Example (twocolumn proof)The Pythagorean theorem states that in a right triangle the sum of its squared legs equals the square of its hypotenuse The Pythagorean theorem is one of the most wellknown theorems in mathematics and is frequently used in Geometry proofs There are many examples of Pythagorean theorem proofs in your Geometry book and on the Internet• Identify similar triangles inscribed in a larger triangle • Evaluate the geometric mean • Find the length of an altitude or leg using the geometric mean • Identify and use the ratios involved with isosceles right triangles • Identify and use the ratios involved with triangles



The Easy Guide To The 30 60 90 Triangle




30 60 90 Triangle Definition Theorem Formula Examples
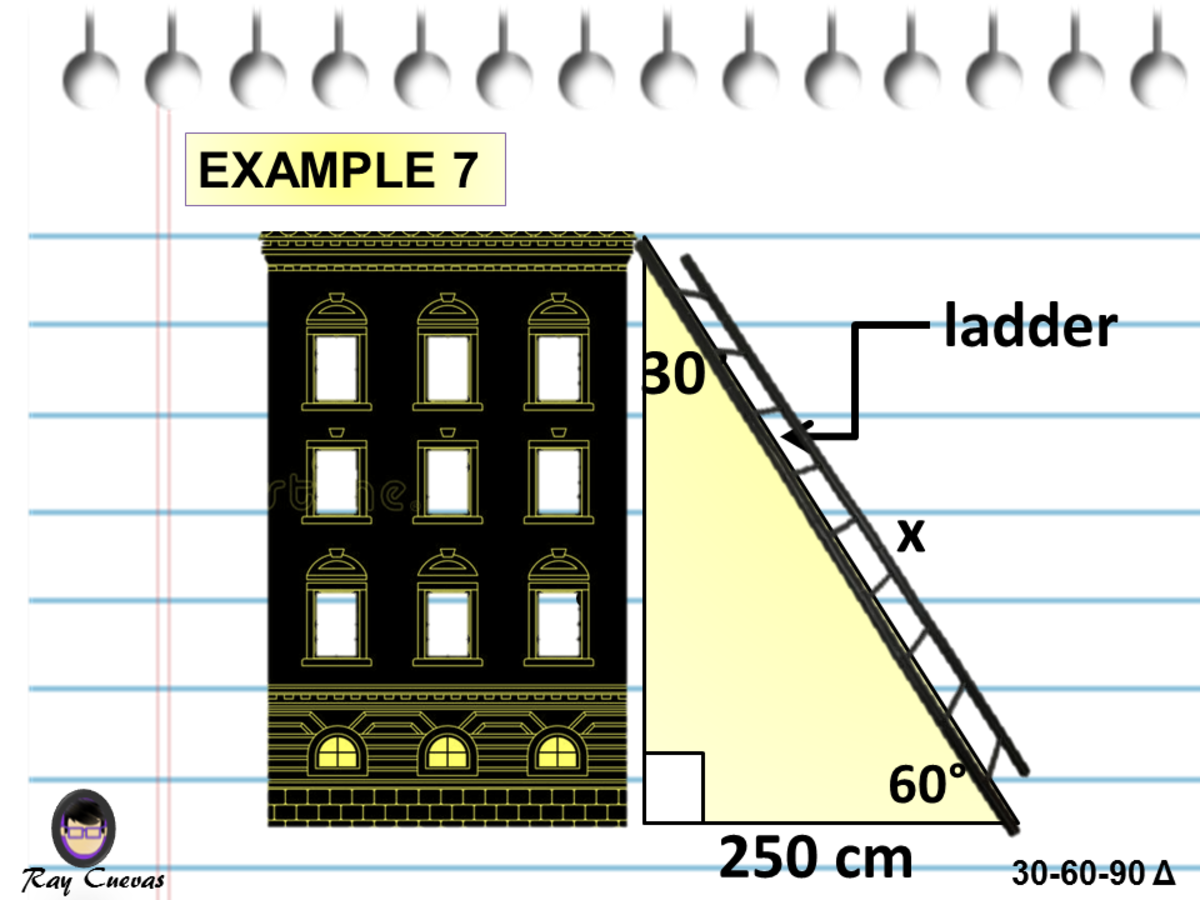
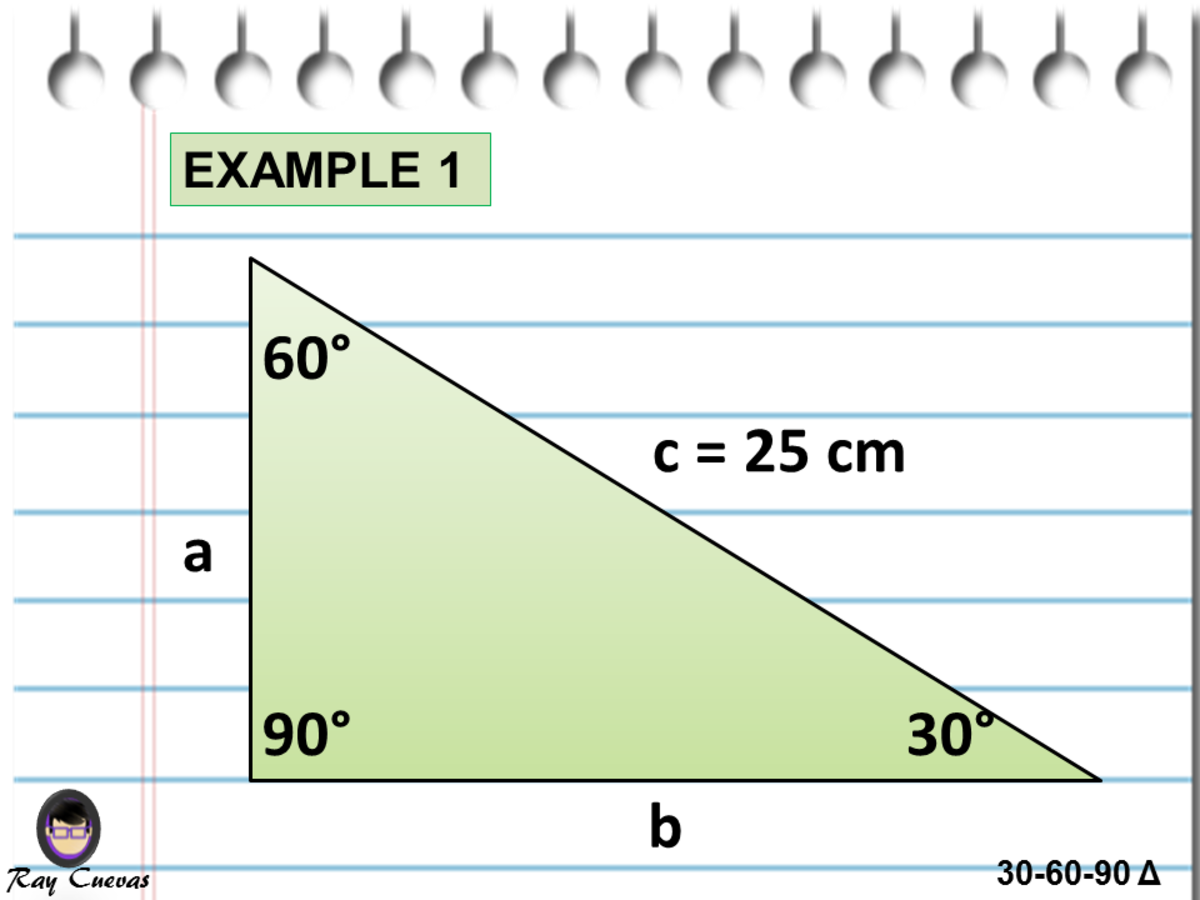
The 30°–60°–90° triangle is the only right triangle whose angles are in an arithmetic progression The proof of this fact is simple and follows on from the fact that if α, α δ, α 2δ are the angles in the progression then the sum of the angles 3α 3δ =Example of 30 – 60 90 rule Example 1 Find the missing side of the given triangle As it is a right triangle in which the hypotenuse is the double of one of the sides of the triangle Thus, it is called a triangle where smaller angle will be 30 The longer side is always opposite to 60° and the missing side measures 3√3 units in 60° x = 223, y = 22 12) u293 v 30° u = 58, v = 29 13) a36 b 60° a = 243, b = 123 14) x y 43 30° x = , y = 12 15) xy 45 60° x = 90, y = 453 16) x 323 y 30° x = 64, y = 32 17) 40 x y 30° x = 3, y = 18) x 333 2 y 30° x = 33, y = 33 2



30 60 90 Right Triangle Side Ratios Expii



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
A right triangle has a leg with a length of 18 and a hypotenuse with a length of 36 Bernie notices that the hypotenuse is twice the length of the given leg, and decides it is a triangle (a) How does Bernie know this a triangle? The "square" at the vertex of the angle indicates that it is 90 degrees A triangle can be determined to be a right triangle if the side lengths are known If the lengths satisfy the Pythagorean Theorem (a2b2=c2) then it is a right triangle How do you find aIn a triangle, the ratio of the sides is always in the ratio of 1√3 2 This is also known as the triangle formula for sides yy√32y Let us learn the derivation of this ratio in the triangle proof section Consider some of the examples of a degree triangle with these side lengths



30 60 90 Triangle Definition Formulas Examples




30 60 90 Right Triangles Ck 12 Foundation
Right Triangles, Pythagorean Theorem and , DRAFT 2 years ago by peggyrenier Played times 0 I have been given the short leg in this triangle How do I find the length of the hypotenuse? Because this is a triangle and the hypotenuse is 30, the shortest leg will equal 15 and the longer leg will equal 15√3 No need to consult the magic eight ball–these rules always work Why it Works ( Triangle Theorem Proof)Special Right Triangles Proof We will now prove the facts that you discovered about the and the right triangles AND we will use the Pythagorean Theorem to do this!




The 30 60 90 Triangle Topics In Trigonometry




30 60 90 Triangle Theorem Ratio Formula Video
Lesson 54 triangle example problem




Special Right Triangles Proof Part 1 Video Khan Academy



30 60 90 Triangle Definition Theorem Formula Examples



The Easy Guide To The 30 60 90 Triangle




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com



The Easy Guide To The 30 60 90 Triangle




30 60 90 Right Triangle Side Ratios Expii



30 60 90 Triangle Sides Examples Angles Full Lesson




30 60 90 Triangle Theorem Ratio Formula Video




45 45 90 Triangle Theorem Rules Formula Video Lesson Transcript Study Com



What Are The Side Ratios For A 30 60 90 Triangle Quora



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math




30 60 90 Triangle Explanation Examples




30 60 90 Triangle Theorem Ratio Formula Video



The Easy Guide To The 30 60 90 Triangle



1




30 60 90 Triangle Calculator Formula Rules
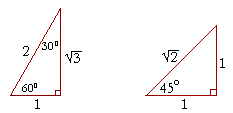



The 30 60 90 Triangle Topics In Trigonometry




State And Prove The Theorem 30 60 90 Please Answer Fast Brainly In



3



What Are The Properties Of A 30 60 90 Triangle Quora




Special Right Triangles Interactive Notebook Page Math Methods Teaching Geometry Teaching Math




30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangle Theorem Ratio Formula Video




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




Special Right Triangles Fully Explained W 19 Examples



Special Right Triangles Proof



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Right Triangles Lesson Geometry Concepts Youtube




30 60 90 Triangles Hd Youtube
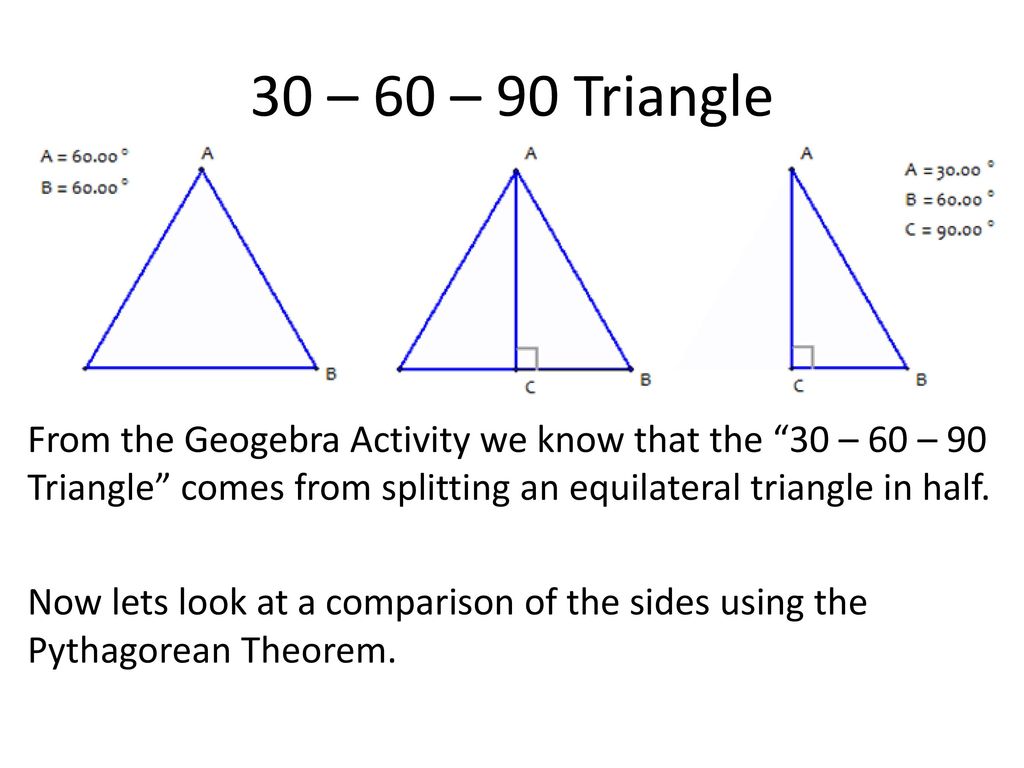



Special Right Triangles Ppt Download



The 30 60 90 Triangle Topics In Trigonometry
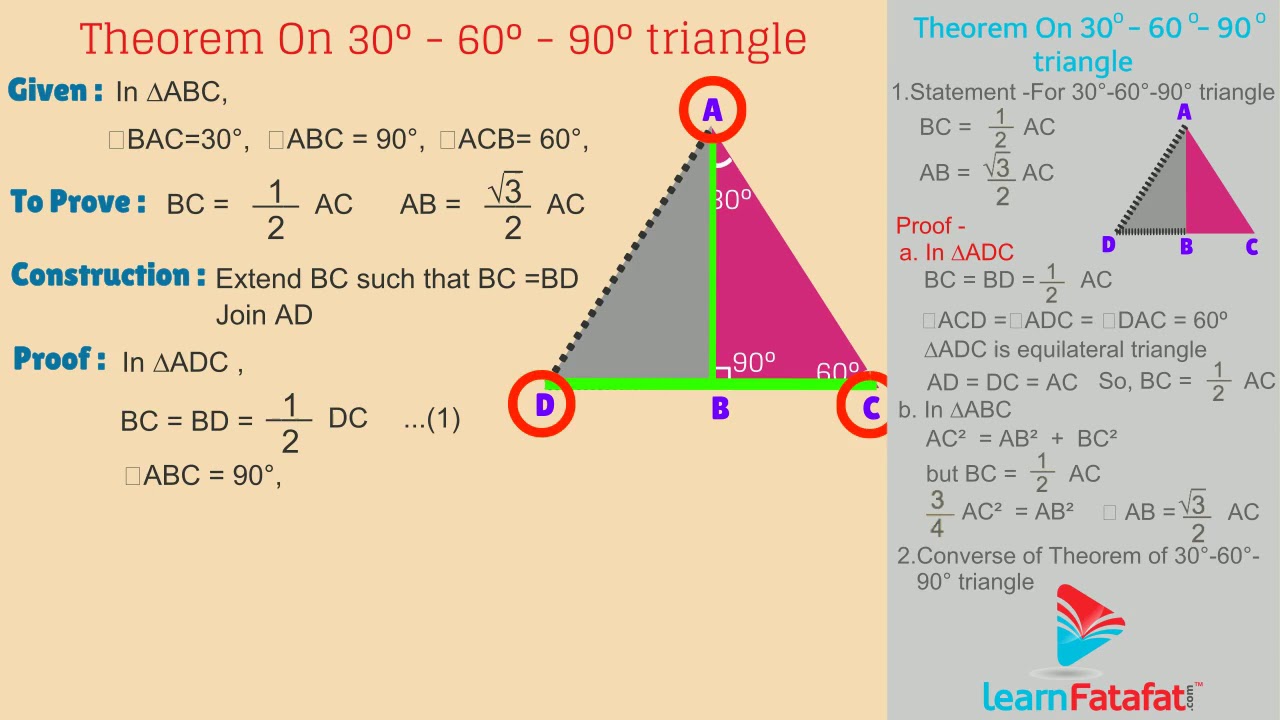



Pythagoras Theorem On 30 60 90 Triangle Youtube




The Complete Guide To The 30 60 90 Triangle




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Theorem Ratio Formula Video




5 30 60 90 Triangles Geometry15a



30 60 90 Triangle Definition Formulas Examples



1




How To Use The Special Right Triangle 30 60 90 Studypug
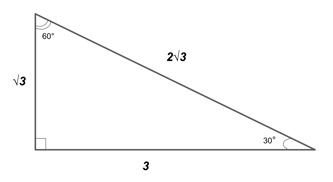



The Easy Guide To The 30 60 90 Triangle




30 60 90 Triangle Theorem Properties Formula Video Lesson Transcript Study Com




30 60 90 Triangle Definition Theorem Formula Examples




30 60 90 Triangle Definition Theorem Formula Examples
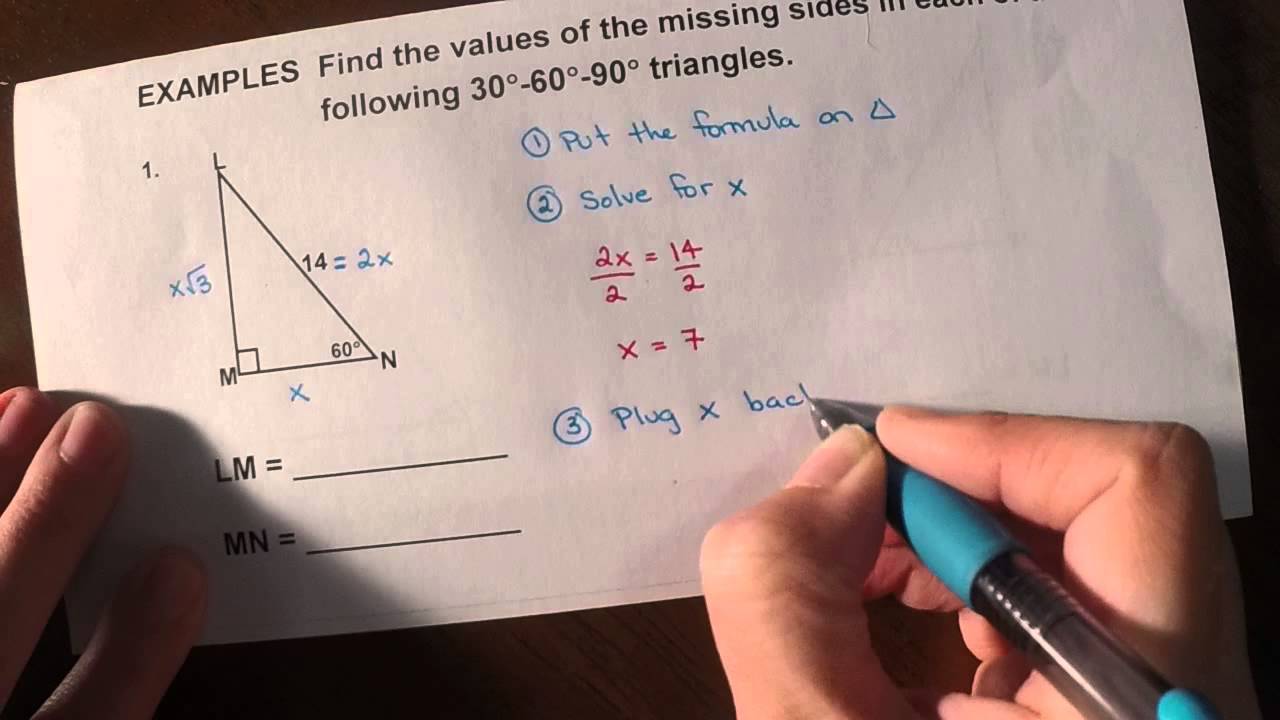



30 60 90 Triangles Youtube




How To Prove 30 60 90 Triangle Theorem 30 60 90 Theorem Youtube
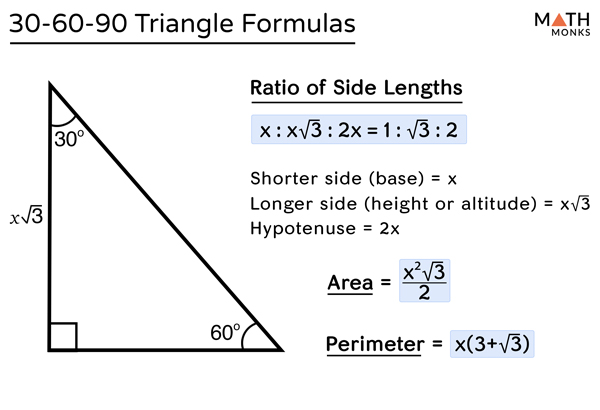



30 60 90 Triangle Definition Formulas Examples




30 60 90 Triangle Rules Sides Ratio Of A 30 60 90 Triangle Video Lesson Transcript Study Com
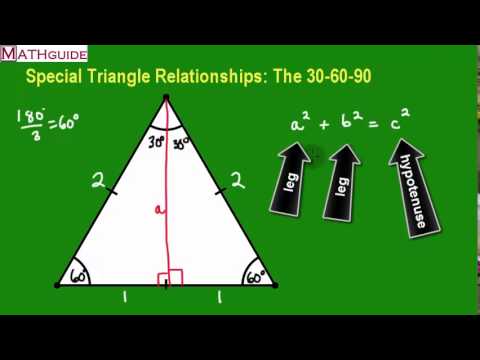



Deriving The 30 60 90 Special Right Triangle Youtube
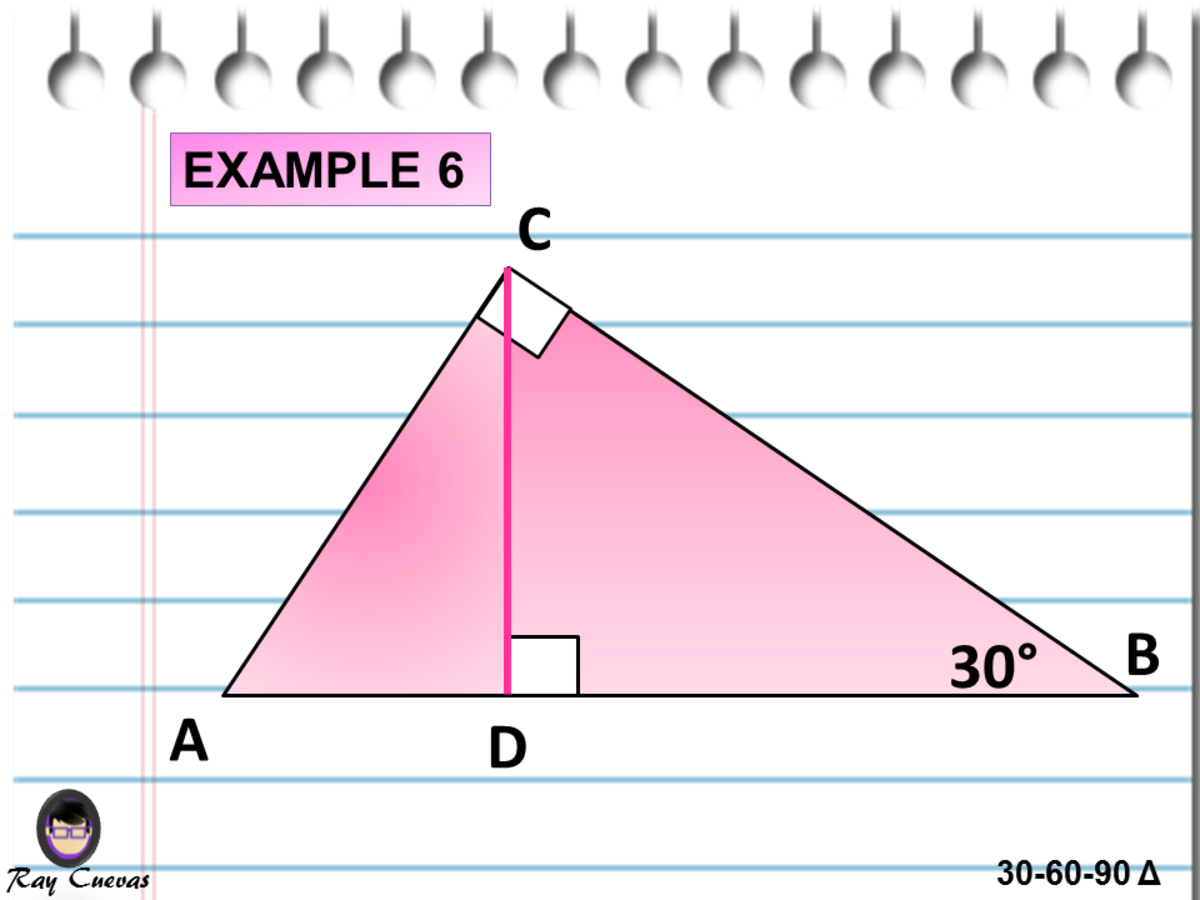



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
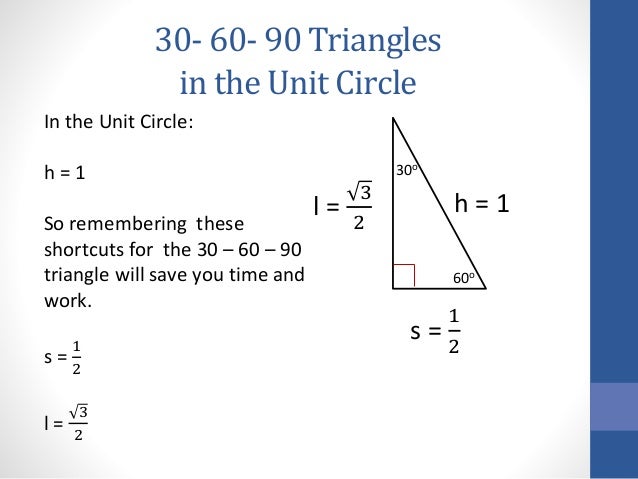



30 60 90 Triangles
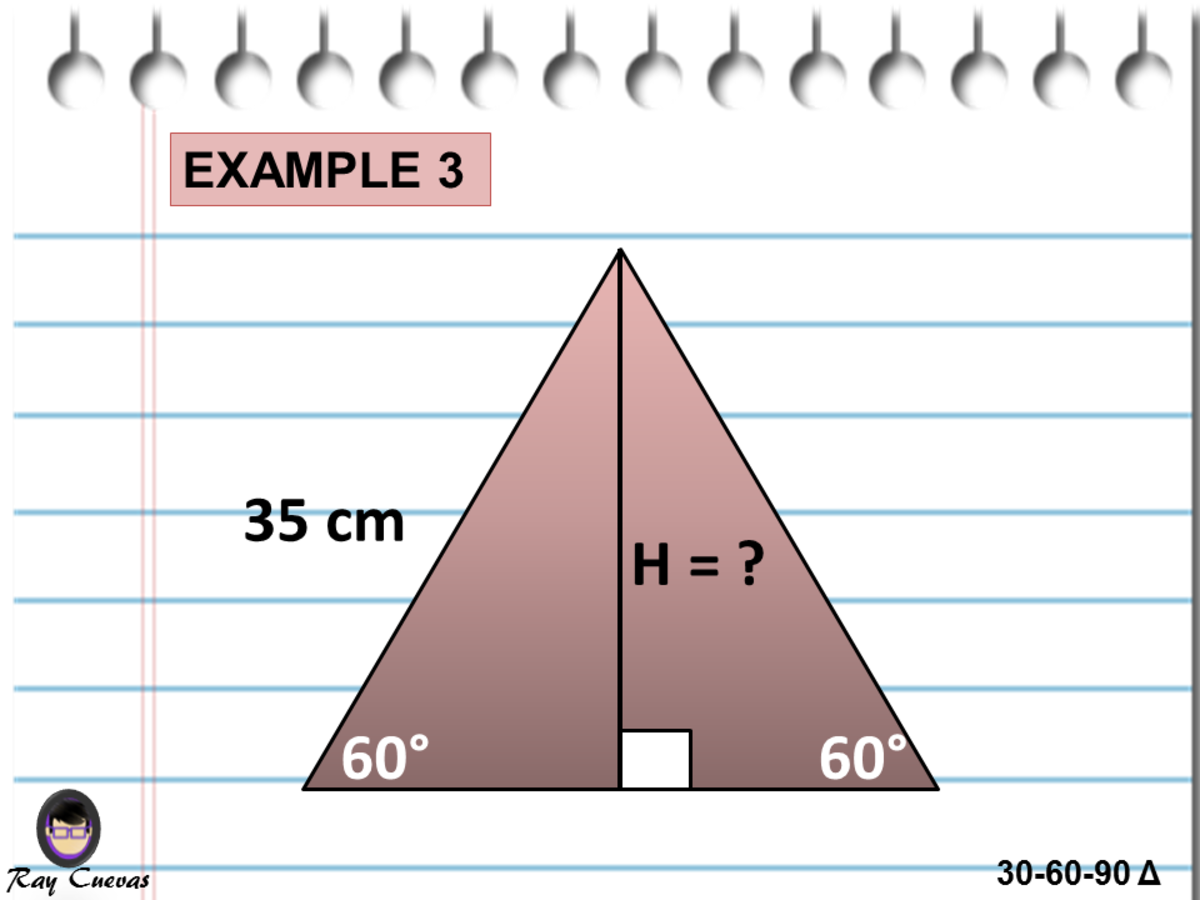



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation
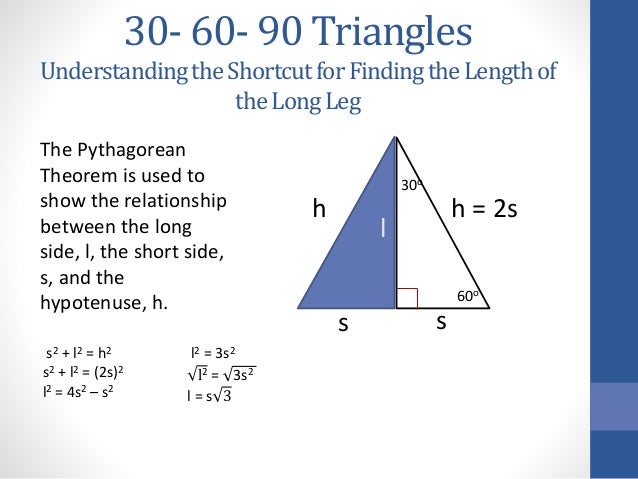



30 60 90 Triangles




Pythagoras Theorem Class 10 Chapter 2 Part 1 Pythagorean Theorem 30 60 90 Triangle Youtube
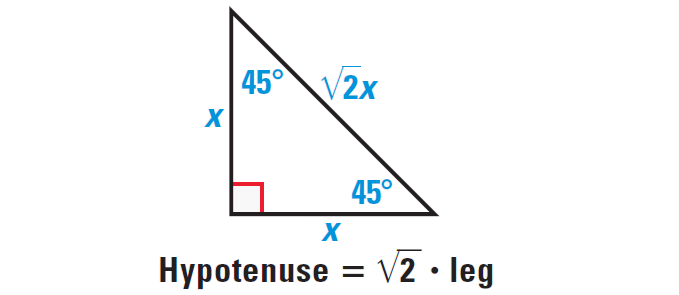



Theorems About Special Right Triangles
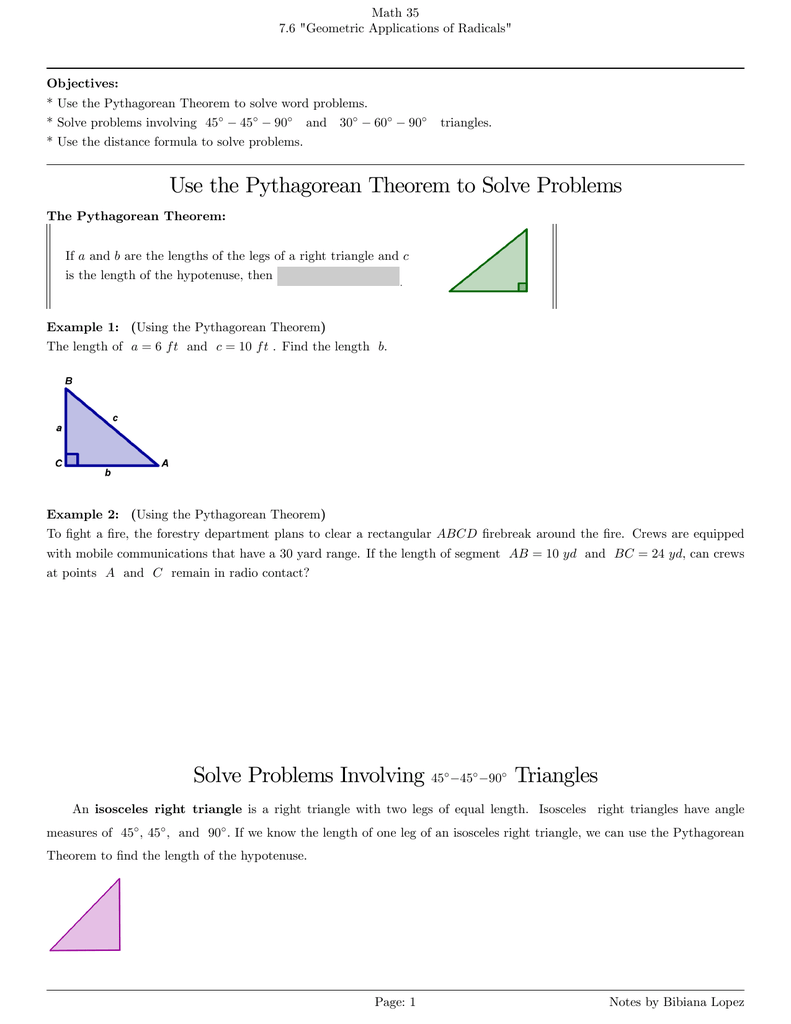



Use The Pythagorean Theorem To Solve Problems Solve Problems
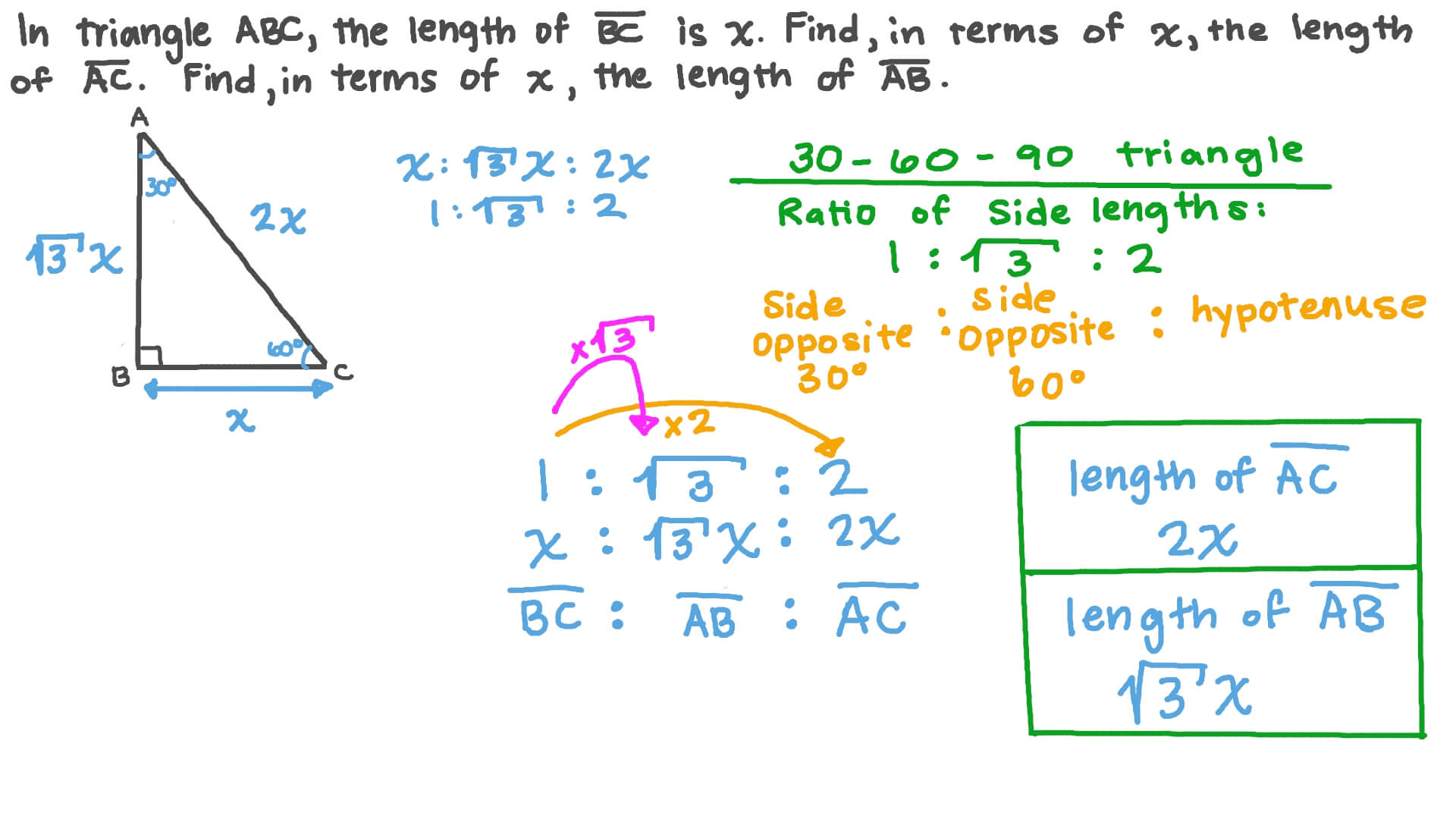



Question Video The Side Lengths Of 30 60 90 Triangles Nagwa




The Converse Of The Pythagorean Theorem And Special Triangles Geometry Right Triangles And Trigonometry Mathplanet




30 60 90 Triangle Theorem Ratio Formula Video




How To Work With 30 60 90 Degree Triangles Education Is Around
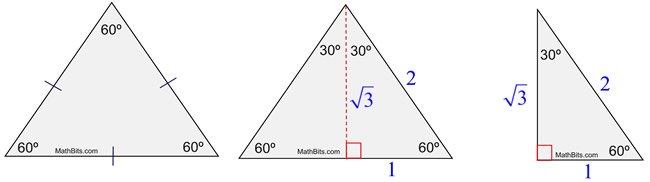



Special Right Triangle 30 60 90 Mathbitsnotebook Geo Ccss Math



Special Right Triangles Proof




30 60 90 Right Triangles Solutions Examples Videos




30 60 90 Triangle Explanation Examples



1
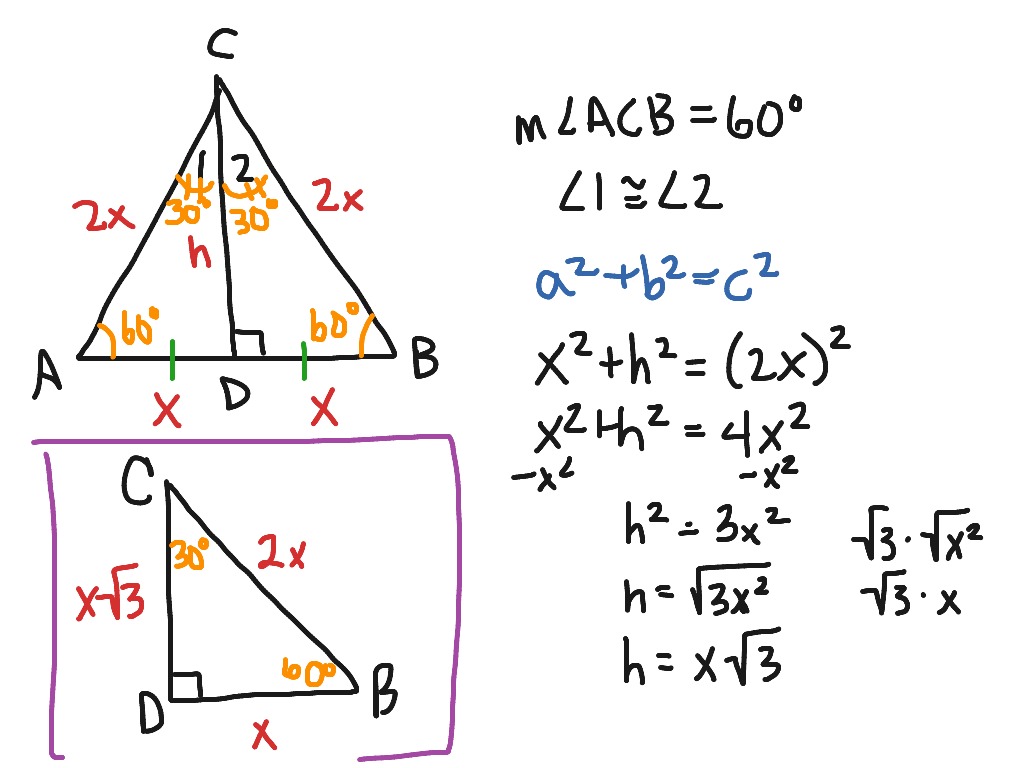



Converse Of 30 60 90 Theorem Off 76 Www Berlinkafe Com




Special Right Triangles Section 9 7 Pages Adam Dec Section 8 30 May Ppt Download
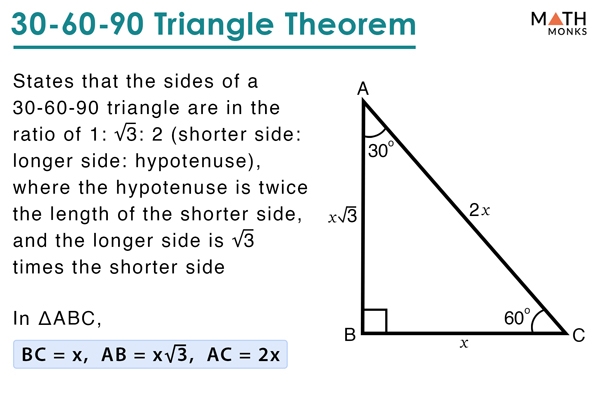



30 60 90 Triangle Definition Formulas Examples




Ppt 30 60 90 Right Triangles Powerpoint Presentation Free Download Id




Learn About The 30 60 90 Triangle Caddell Prep Online




Points Ba Gusto Mo Pasagot Please Wag Mo Sayangin Points Na Ibibigay Ko Quiz On 30 60 90 Right Brainly Ph



Class Notes




Proof Of 30 60 90 Theorem Geometry Maths Ii Standard 9th Youtube
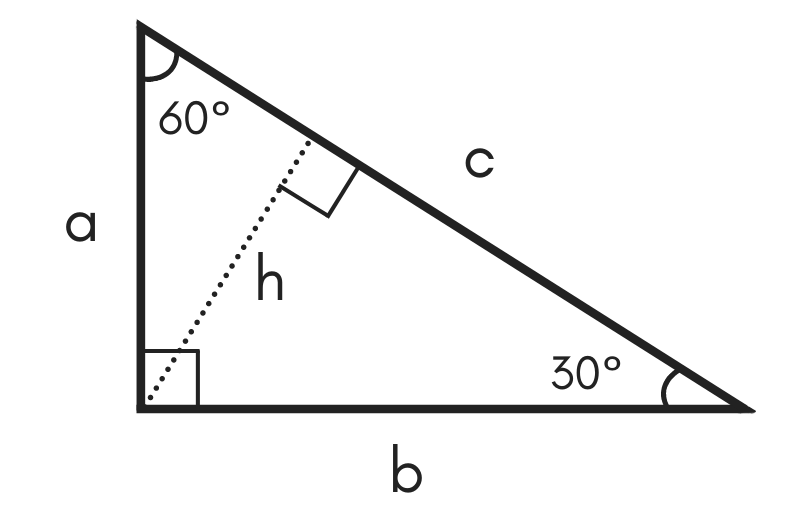



30 60 90 Special Right Triangle Calculator Inch Calculator




A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




30 60 90 Triangle Calculator Formula Rules
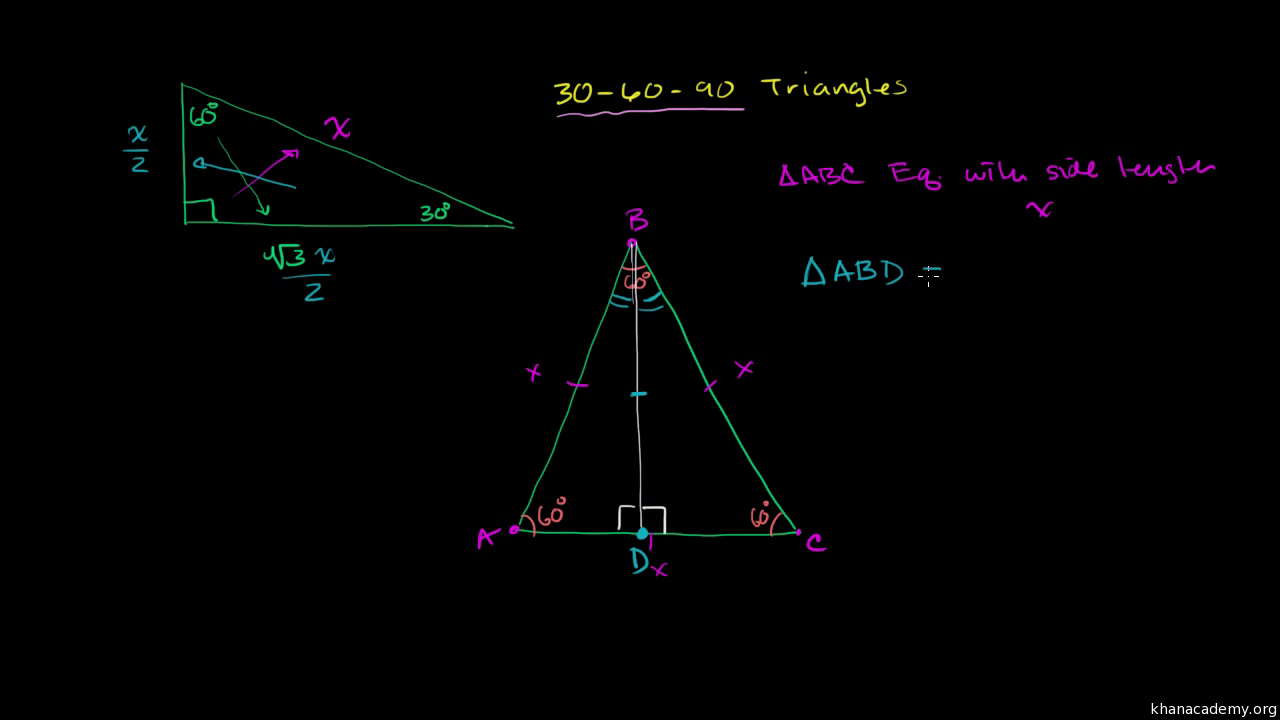



Special Right Triangles Proof Part 1 Video Khan Academy




30 60 90 Triangle Theorem Ratio Formula Video
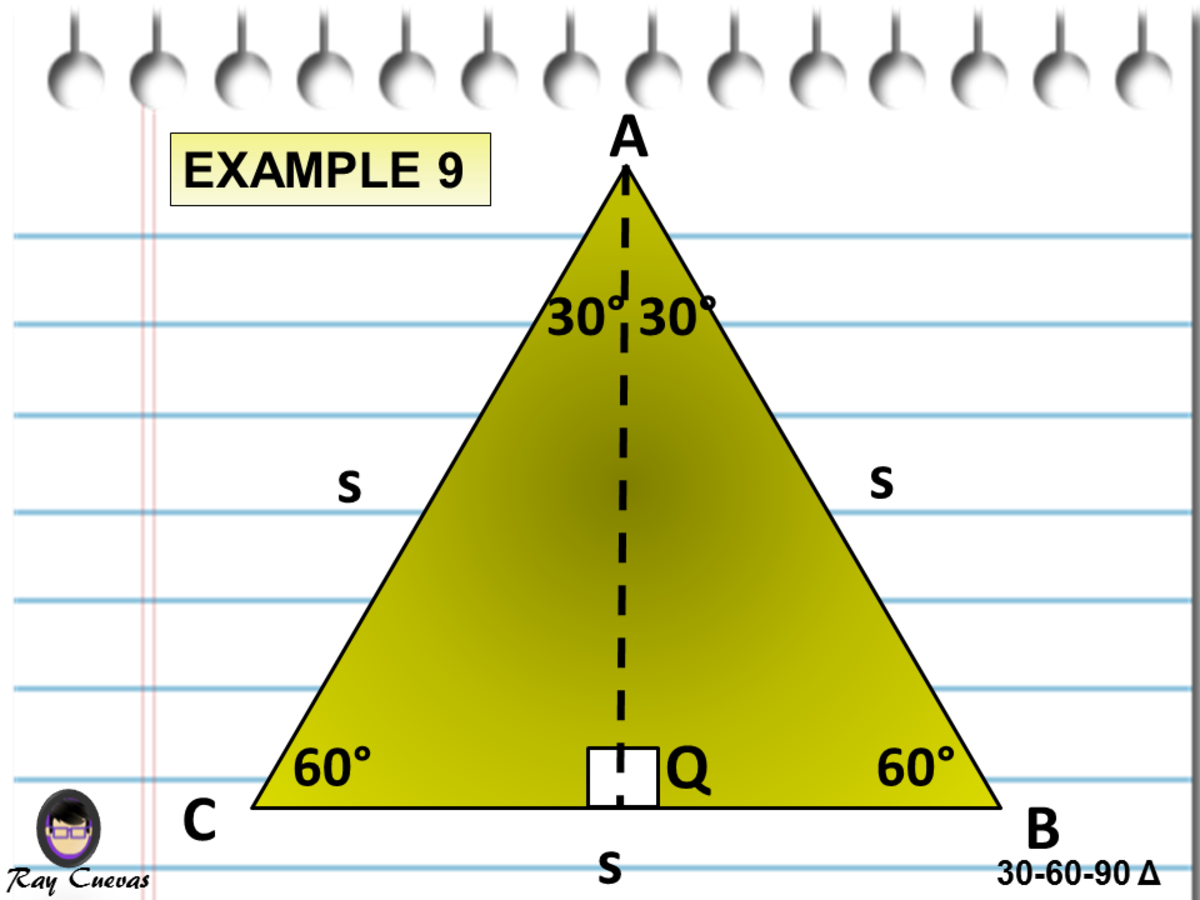



A Full Guide To The 30 60 90 Triangle With Formulas And Examples Owlcation




What Is Converse 30 60 90 Triangle Theorem Brainly In



0 件のコメント:
コメントを投稿